数据结构和算法
数据结构,主要需要掌握,数组,栈,队列,链表,树(二叉树)
数组
这是一种最简单,最基础的数据结构,在 js 中是原生支持的
栈
在 js 中,栈和队列都没有原生的实现,需要依赖数组实现
栈是后进先出的一个数据结构,所以只能用到 pop 和 push 完成增删
class Stack {
constructor() {
this.arr = [];
}
push(item) {
this.arr.push(item);
}
pop() {
this.arr.pop();
}
}队列
队列是先进先出的数据结构,所以只要用 push 和 shift 完成增删
class Queue {
constructor() {
this.arr = [];
}
push(item) {
this.arr.push(item);
}
shift() {
this.arr.shift();
}
}链表
不同于以上的三种线性数据结构(有序的),链表中,数据单位的名称叫做 结点 ,而结点和结点的分布,在内存中可以是离散的,如图:

每一个结点的结构都包含了两部分内容:数据域和指针域。js 中的链表,是以嵌套的对象的形式来实现的。
{
// 数据域
val: 1,
// 指针域,指向下一个结点
next: {
val:2,
next: ...
}
}用图片表示为
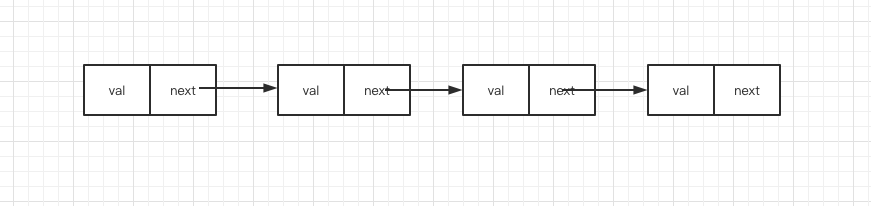
然后就是需要使用类来实现链表结点
class ListNode {
constructor(val) {
this.val = val;
this.next = null;
}
}在生成链表数据时,需要传入 val(数据域对应的值)、指定 next(下一个链表结点)
const node = new ListNode(1);
node.next = new ListNode(2);以上,就创建出了一个数据域值为 1,next 结点数据域值为 2 的链表结点
树
树结构就是由自然界中的树演变而来,我们将自然界中的数抽象,就得到了计算机中的树结构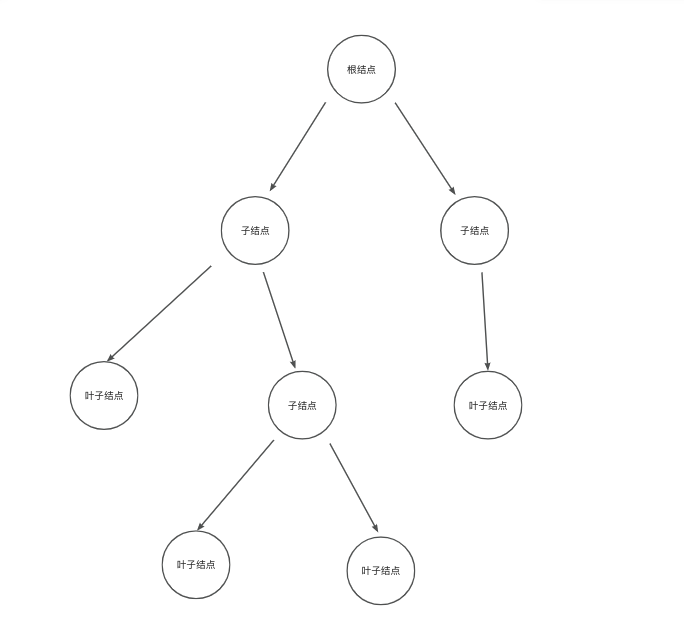
结合这张图,我们来讲解树的关键特性和重点概念。要牢记以下几点:
- 树的层次计算规则:根结点所在的那一层记为第一层,其子结点所在的就是第二层,以此类推。
- 结点和树的“高度”计算规则:叶子结点高度记为 1,每向上一层高度就加 1,逐层向上累加至目标结点时,所得到的的值就是目标结点的高度。树中结点的最大高度,称为“树的高度”。
- “度”的概念:一个结点开叉出去多少个子树,被记为结点的“度”。比如我们上图中,根结点的“度”就是 3。
- “叶子结点”:叶子结点就是度为 0 的结点。在上图中,最后一层的结点的度全部为 0,所以这一层的结点都是叶子结点。
二叉树结构
二叉树是指满足一下要求的树:
- 它可以没有根节点,作为一颗空树存在
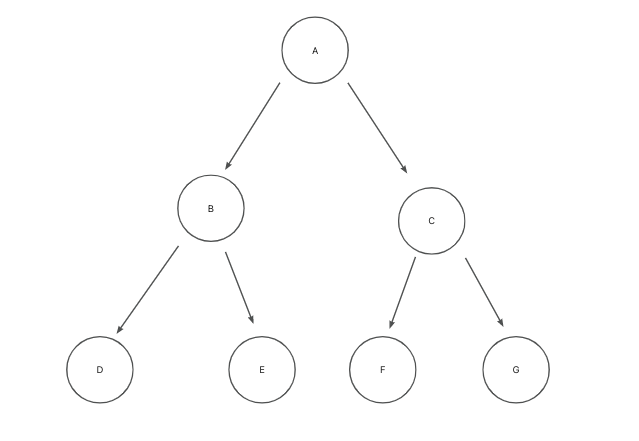
- 它如果不是空树,那么必须由根节点。左子树和右子树组成,且左右子树都是二叉树。如下图:
注意,二叉树不能被简单定义为每个结点的度都是 2 的树。普通的树并不会区分左子树和右子树,但在二叉树中,左右子树的位置是严格约定、不能交换的。对应到图上来看,也就意味着 B 和 C、D 和 E、F 和 G 是不能互换的。
二叉树编码实现
在 JS 中,二叉树使用对象来定义。它的结构分为三块:
- 数据域
- 左侧子结点(左子树根结点)的引用
- 右侧子结点(右子树根结点)的引用
在定义二叉树构造函数时,需要将左侧子结点和右侧子结点都预置为 null
class TreeNode {
constructor(val) {
this.val = val;
this.left = this.right = null;
}
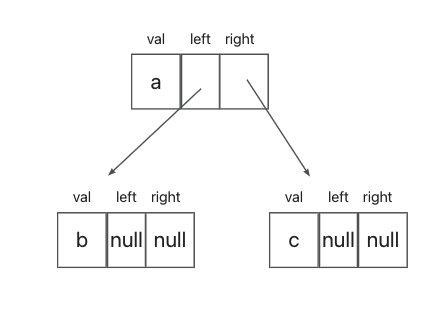
}当需要新建一个二叉树节点时,直接调用构造函数、传入数据域的值就行了:
const node = new TreeNode("a");
node.left = new TreeNode("b");
node.right = new TreeNode("c");如此便能得到一个二叉树,从结构上来看,它长这样